- Главная
- О Группе компаний
- Продукты
- Безопасность
- Комплексная автоматизированная информационная система «Безопасный город»
- ПО потокового вещания видео и ведения архива «Медиасервер»
- ПО для создания распределенных систем IP-видеонаблюдения «SmartStation»
- Программно-аппаратный комплекс для создания систем видеонаблюдения «ТелеВизард-HD»
- ПО для создания систем видеонаблюдения «Компас»
- Здоровье
- Блокчейн
- Безопасность
- Наука
- Отзывы
- Контакты


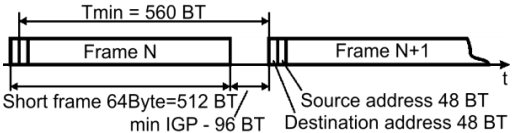
Energy efficient algorithm for lookup-tables on mobile devicesSergey Makov(a), Vladimir Frantc(a), Viacheslav Voronin(a) Igor Shrayfel(a), Vadim Dubovskov(a) and Ilya Svirin(b); Abstract In this paper we present a novel approach for energy efficient hash table design. Hash table is a common approach to build associative arrays, database indexes and various kinds of program-defined caches. These data structures play a crucial role in modern feature-rich mobile applications. It in turn leads to significant power consumption associated with their use. However, modern hashing techniques are suffered from large probability of collision in the case of hash size acceptable for mobile devices. This makes it necessary to perform additional energy-inefficient memory access operations to resolve these collisions. We propose hashing technique with lower probability of collision for the hash of the same size. We show that unlike existing collision free approaches our hashing method has a much broader area of applicability. To support these claims both theoretical and experimental studies are presented. Experimental comparison with existing approaches has shown significant improvement of energy- efficiency for common applications. Keywords — hash table, bridging, filtering table, frame switching, collision probability Introduction Mobile devices should work fully autonomously in autonomous mode using portative power supplies only. It makes their energy efficiency an extremely important problem. There are few ways to improve energy efficiency. One of them is to improve microelectronics technology. Decreased electrical capacity of the gate leads to reduction of power consumption per each gate in digital circuit. It can be achieved by reduction of gate size. [1] Another way is dynamical control of voltage supply and clock frequency of digital circuits according to perfomed tasks. This approach suggests compliance of operating systems and applications for mobile devices to given requirements [2]. The main mechanism is to switch the mobile device in “sleep mode” that have to be supported by operating system. [3] All these ways are universal and independent on algorithms used within applications and operating system functions. In order to ensure high energy-efficiency, algorithms targeted to mobile devices should be developed with minimal memory and computational requirements. This is general requirement for all algorithms. Other requirement is speed. In many cases these requirements cannot be achieved simultaneously. One of the common types of algorithms is ones based on lookup-tables. Some applications require to deteimine if some data point belong to one or another group based on some criteria. For instance, it can be classification of pictures according presence of particular person or smiling faces in it. Another important example is separation of descriptors according to some features. In some applications there is a need to have ability to modify behavior and update its lookup-tables when objects transit from one class to other or when infomation about object5s class These tasks are usually being solved by self-learning lookup- tables. Thafs why development of methods for lookup-table design and efficient algorithms to update or search information within the table is an actual goal. Some of application dependent of lookup-tables are supposed to work in real-time. In such situations the time to update data or to perform a search within it is limited. Quite often this time may be about few microseconds. This is the case for packet switching or routing with use of self-leamed lookup-tables. All operations in this type of tables should be performed in time interval between two packets as shown on figure 1 for Ethernet. In case of on-the- fly processing the time to search data in the table for correct switching or routing could be limited by nanoseconds.
Figure 1. Time of processing algorithm The most efficient way of lookup-tables design is hashing tables [4]. However, this approach has a disadvantage - there is possibility for several different search keys to have equal hash. This situation is called “collision”. There are many was to resolve collisions in hashing tables. All of them take additional time and computational resources. Not resolved collision is the cause of wrong search result. In case of classification task it means false negative or false positive results. In this paper we discuss methods of hashing lookup-table design for applications in which is able to have non-zero probability of false positive or false negative results of search. We show that convenient hashing tables design methods have lacks and propose method to improve hashing table efficiency. Also we propose the method to find the “ideal” hashing strategy for applications in which searching results should be exact. Hashing efficiency The method of blocks is convenient method for hashing tables collision resolving. According to this method for each hash value several cells is allocated to store search key. In the case of collision the search continues in next cell until the match is found or an empty cell is reached. We have shown that this method does not eliminate the probability of collision, but rather provides a reduction to an acceptable value. To assess the efficiency of table design method we compare amount of memo^ to store the lookup- table and the probability of non-resolved collision. The collision probability is the ratio of number of all possible combinations of searching keys that give us collision Q and the number of all possible combinations of searching keys W:
To find the collision probability let’s make following definitions: r - the number of possible hash values; m - the number of existing at the moment searching keys; k - the number of cells in the table for one hash value k<l. Below we use the following denotes:
The set В is a subset of A and it consists of all existing Let’s derive an expression to count all allowable sets
Suppose that inequality (3) is satisfied. In this case if k=0 then m=0 and the only one allowable set is B=Ø . It means
Let’s consider the case when k≥1. For every allowable set В we will take
Let’s find the range of values
or
Opposite is also true. For each integer 5 from band (4) may be found allowable set В satisfied the condition: take s -elements subset TB of set {1,2,...r}; if TB is not empty, for each i∈TB take k-elements set Bi from Ai; tak suppose The first procedure can be accomplished in
From (3) and (4) it is clear that all values denoted as Let’s derive expressions for collision probability for lookup-tables designed by convenient method. Using (1),(2) and (5) we will have:
For k=2 we have:
For k=4
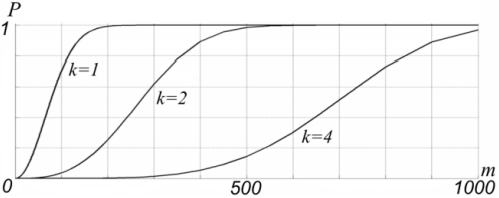
As you can see, the expression becomes more difficult with the growth of the number of cells in a block. For example for the Ethernet MAC-addresses r - I is equal to 248. For 10-bit hash r=1024. Fig. 2 shows dependence of the collision probability from the number of nodes in net m of blocks k=l, k=2 and k=4. For this example the required amount of memory for lookup-table is 256Kbits. In the system proposed by the McNeil patent [5] with a memory amount of 8 Mbit,a 15-bit hash was used. We have calculated the probability of collisions for the system. It was approximately 10-7 for 1000 network’s nodes.
Figure 2, Collision probability for convenient method Thus even for method of blocks the collision probability do not reach zero. We can provide acceptable level of collision probability only by use of different methods to reduce this probability, such as parallel hashing or adaptive hashing. Proposed method Any classification database can be represented as set of labels which associate objects to particular class. For example, in case of use of hashing table as filtering table within network switch, we can split filtering table to several ones according to the number of switch ports. We propose to exclude the storage of the searching keys in the table. According to proposed method, only the infomation on the object’s class should be stored in the table. We propose to store two flags in lookup-table. One of the flags has non-zero value when an object belongs to a given class. In other words,searching key is belonging to the set of existing keys. The other flag is nonzero if object is not of this class. Thus the amount of required memory to store the table will decrease. But we will not be able to use a mechanism of collision resolving. The collision in this case of lookup-table design takes the place only if both flags have non-zero value for the same hash. So we should estimate the collision probability for proposed method. To solve this problem we use previous definitions with some additions: m - the number of existing at the moment searching keys belonged to the class; n - the number of existing at the moment searching keys not belonged to the class. Lefs suppose set В contains searching keys belonged to the class and set C is consisted of searching keys not belonged to the class. The elements of set В are randomly selected from set A (all existing searching keys). And the elements of set C are selected from the set A\B . All selected elements have same probability to be chosen. We can construct sets of hash values for sets C and B. It is:
The condition of collision to come upis following:
Let’s find the probability that intersection of L and M is empty. Let’s call “good” any pair of sets В and C if they provide that event. Then probability of collision is a probability of opposite event. To solve this problem let’s solve an auxiliary problem. Let’s denote as tr(m;l) or shorter as tr the number of m-elements subsets В of set A such that for each Suppose к as minimal integer number greater or equal to
By definition |A| = rl. Then with r<k and use (7) If r>m, any В c A intersecting with every Ai, 1≤i≤r consists not less than m elements and not more m elements. That means tr = 0. Lefs prove (8) for k≤r≤m. If
This is equal to the number of all possible m-elements subsets of set A (from (7) follows kl≥w). Because of kl-m<l (from (7)) all the subsets intersecting with each Ai, 1≤i≤k . Thus we prove (8) for r=k. Lefs suppose that (8) is true for any integer k≤r≤j. Here j-is integer number form range k≤j<m. . Lefs prove (8) for the case of r=j+1. From rl= (j+1)l-elements set A we can construct
It is clear that qp=0 for p>j+1. Besides,because of tp=0 with p<k: (as was proved before) qp=0 with same p. Thus
Here The sum (10) consists of With (9) and with equation
Using the mathematical induction lefs replace r to p within (8):
Then (11) can be rewritten as:
The last sum of this expression can be simplified:
Thus
with r=j+1. Thus expression (8) is true for k≤r≤m. The ranges of possible values of λ and μ are following:
Here, s is the least integer that greater or equal of
which means k+s≤r (13) To provide a positive value of collision probability it is necessary and sufficient to satisfy condition (13). Then for each solution
So the whole number of such pairs is equal
Thus we have an expression to find probability of collision for proposed method:
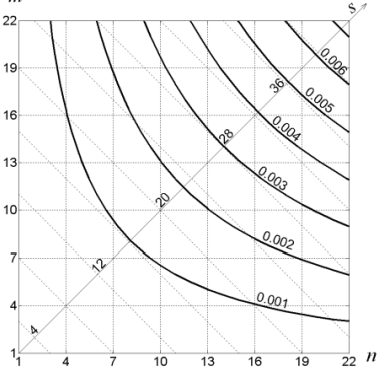
Figure 3 shows the results of calculating collision probability for proposed method. The bold lines show values of the probability in dependence on n and m. The diagonal axis 5 is the sum of n and m. Here we can see that for equal 5 the worst case in since of collision probability is when n=m
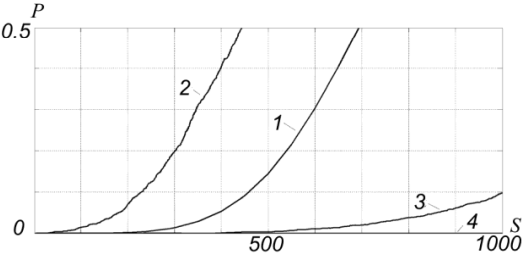
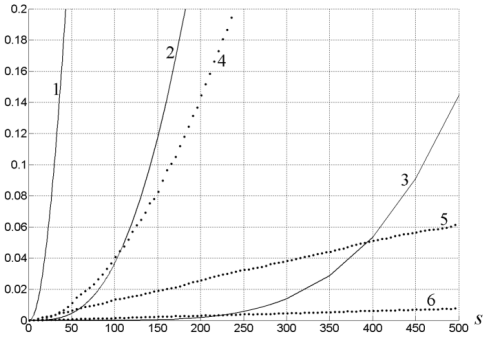
Figure 3, Collision probability for proposed method To compare the probability of collision for convenient and proposed methods we calculate collision probability of lookup-table without keys storing with the same size as in the previous example (256Kbits). The figure 4 shows results of comparison.
Figure 4, Collision probability comparison On the figure 4 s is a summary number of keys. Line 1,2 and 3 show dependence of collision probability for convenient method of hashing tables design like in previous example. Line 3, 4 and 5 Using of parallel hashing can give dramatic improvement of method efficiency as shown in [6]. In the case of using parallel hashing collision came up when we get collision in all of parallel tables. The condition of collision is following:
According (15) we calculated collision probability and compared it with previous example.
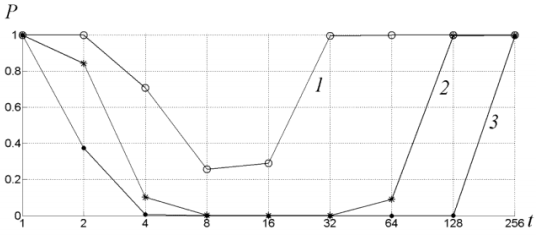
Figure 5, Parallel hashing collision probability comparison The results are shown on figure 5 were got with the following conditions: 12-bit hash, 8 parallel tables, 4-bit record length in each table, no searching key storing (line 4). Summary required memory size is 128KBit. Line 1 for convenient method (10-bit hash, 64-bit record length, total 256 Kbit). Line 2-2 parallel tables, no searching key storing, total 32Kbit. Line 3-4 parallel tables, no searching key storing, 64Kbit total. From figure 5 it is clear that even for 4 parallel tables the collision probability is much lower than for the block method. In addition, the total memory size to allocate the tables for proposed method was per 4 times lower than the reference method. With the increasing number of parallel hashed tables up to 8; the tables size was 128 Kbit, and the collision probability was lowered to minimal,as for the reference method,the memory size of the table was 8 Mbit meaning a reduction of 64 times in memory usage. During the studying of relation collision probability of lookup-table table designed by proposed method we found an optimal number of parallel tables for a fixed total memory size, figure 6 shows the dependence of collision probability according to the number of parallel tables. The number of existing keys was S = 1000 and for total memory size of 32 Kbit (line 1),for $4 Kbit (line 2) and for 128 Kbit (line 3). In this figure values near the axis
Figure 6. Optimum of probability These results suggest an optimal number of parallel tables for every fixed total memory size to allocate parallel hash lookup- tables. “Ideal” hashing The ideal hashing or perfect hash function allows to avoid collision at all. To eliminate the lack we propose to combine parallel hashing with a mechanism of perfect hash selection.
here Pt is collision probability for t parallel hash tables before changing the adaptive hash. Thus, if initial collision probability for proposed method was 10-2,in case of collision detection,the first iteration of hash function changing will give us 10-4; next iteration - 10-6 e.c.t. As we can see,the required amount of memory is similar to the proposed method of parallel hashing without searching keys storing, but thanks for adaptive mechanism we can decrease collision probability to required value. Besides we insignificantly los the hash table in the process of changing the adaptive hash function. This is because of we have several other parallel tables that keep working during adaptive table is rebuilt. Conclusions The proposed in the paper approaches to design hash lookup- tables allows dramatic decrease the amount of required memo^ without losing efficiency of lookup-table perfomance. Besides, these approaches are ready to be realized as IP-cores or ASIC microchips that can work with much more lower clock frequency and supply voltage. It can reduce the load to the CPU and main memory of mobile device. Proposed method allowed to reduce the power consumption of network switch up to 4 times is comparison with convenient method. This result was confirmed in stand tests. Acknowledgement This work was supported by Russian Ministty of Education and Science in frame of the Federal Program "Research and development on priority directions of scientific-techno logical complex of Russian Federation in 2014-2020" (contract №14.576.21.0080 (RPMEFI57614X0080)). References
Author Biography Sergey Makov was born in 1978. In 2001 he has graduated Don State University of Service as radio engineer. Since then he is working in the engineering company as designer of telecommunication hardware. He has got PhD in 2011. Since then he has worked as a professor assistant in the department of electronic systems of Don State Technical University. Vladimir Frantc was born in Dushambe, Tadjikistan in 1989. He received his BS in electrical engineering from South-Russian University of economics and service in 2011. He received the M.Sc. degree in technics from Don State Technical University (Russian Federation) in 2013. At the time he is a PHD student at Don State Technical University. His research interests lay in the areas of applied mathematics, digital signal processing and computer vision. Viacheslav Voronin was born in Rostov (Russian Federation) in 1985. He received his BS in radio engineering from the South-Russian State University of Economics and Service (2006),his MS in radio engineering from the South-Russian State University of Economics and Service (2008) and his PhD in technics from Southern Federal University (2009). Voronin V. is member of Program Committee of conference SPIE. His research interests include image processing, inpainting and computer vision. Igor Shrayfel was born in 1958. He received the BS in mathematics from Rostov State University in 1981. Since then he is working as a professor assistant in the department of mathematics of Don State Technical University. He has got PhD in 1986. Vadim Dubovskov was born in 1987. He received his BS in electrical engineering in South-Russian University of economics and service in 2008. He received the M.Sc. degree in technics in Don State Technical University (Russian Federation) in 2010. His research interests are signal reconstruction and sparse representation. Ilya Svirin was born in 1980. He received the PhD. degree in technics in Bauman State Technical University (Russian Federation) in 1999. His research interests are multiwavelets, signal reconstruction and sparse representation. |


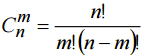 - the number of m -combinations of a set of n elements, for m≥n≥0.
- the number of m -combinations of a set of n elements, for m≥n≥0. 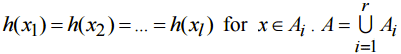 .
.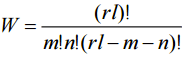 (2)
(2) 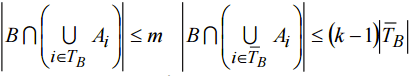

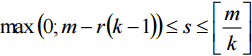 (4)
(4)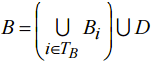 .
.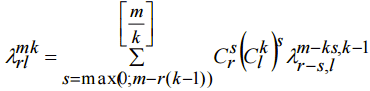 (5)
(5)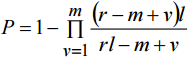
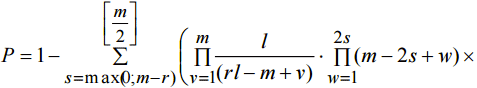
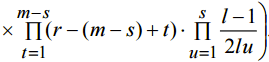
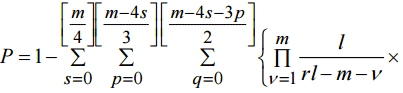
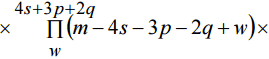
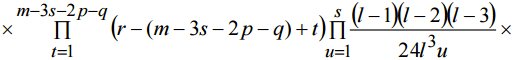
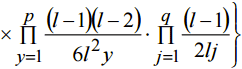
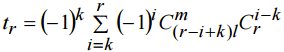 (8)
(8)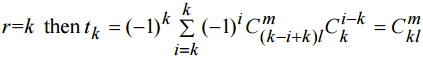 .
.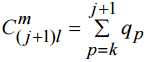 (9)
(9) 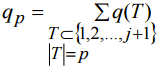 (10)
(10)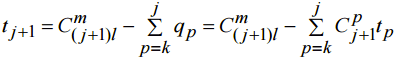
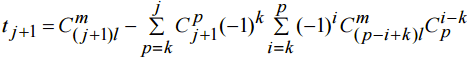 (11)
(11) 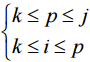
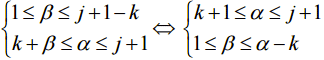
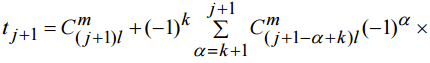
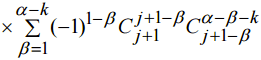
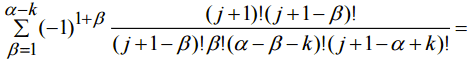
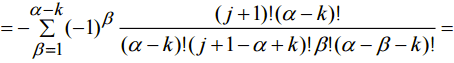
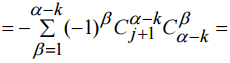
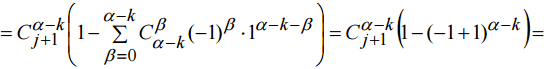
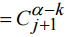
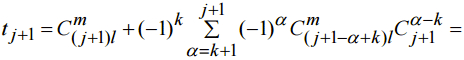
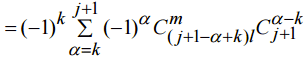 , we have expression (8)
, we have expression (8)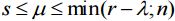 (12)
(12)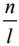 . So the k≤m,s≤n, then (12) have solution if and only if
. So the k≤m,s≤n, then (12) have solution if and only if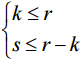
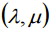 of (12) exists
of (12) exists 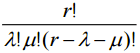 a pair of sets
a pair of sets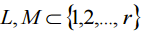 such that
such that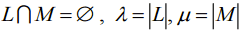 . Each the
. Each the 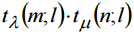 of “good” pair of sets В and C.
of “good” pair of sets В and C.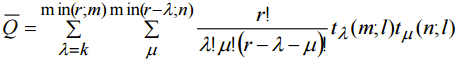
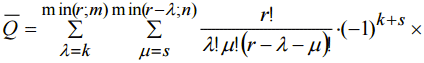 (14)
(14)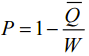
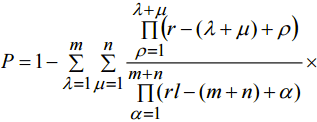
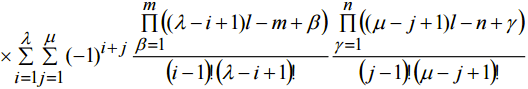
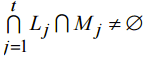 (15)
(15)