- Главная
- О Группе компаний
- Продукты
- Безопасность
- Комплексная автоматизированная информационная система «Безопасный город»
- ПО потокового вещания видео и ведения архива «Медиасервер»
- ПО для создания распределенных систем IP-видеонаблюдения «SmartStation»
- Программно-аппаратный комплекс для создания систем видеонаблюдения «ТелеВизард-HD»
- ПО для создания систем видеонаблюдения «Компас»
- Здоровье
- Блокчейн
- Безопасность
- Наука
- Отзывы
- Контакты


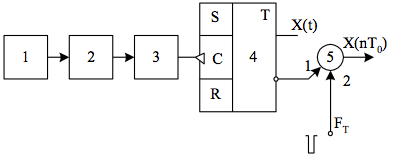
Parameters estimation of random sequence in the stochastic calculating devicesGennady Galustov, Viacheslav Voronin, Sergei Makov Abstract — In this article we introduce the concept of probabilistic binary element provides requirements, which ensure compliance with the criterion of "uniformity" in the implementation of the basic physical generators uniformly distributed random number sequences. Based on these studies, we obtained an analytic relation between the parameters of the binary sequence and parameters of a numerical sequence with the shift register output. I. Introduction In solving problems of simulation one of the main points of the decision is the right choice of quality parameters of the basic random perturbations, from which to a large extent depend on the variance estimates of the output parameters of the models. Recently, very often these problems are used as input to the pseudo-random number sequences, followed by transformation of the statistical characteristics [1]. No additional difficulties arise when it comes to just about measuring the average values or the mean square values or the output of the study of correlations between input and output values of linear systems with constant parameters. The results of such studies depend only on the autocorrelation function of the pseudo-random input signal, which in this sense is very good approximation of white noise. However, the results of statistical analysis of nonlinear systems can have a marked effect of the distribution of the second and higher orders used by the pseudo-random noise signal, and these are not necessarily Gaussian distribution [2]. In addition, the law of distribution of the output of the linear system under the influence of pseudo-random noise is not derived theoretically, but it is difficult to assess the dispersion of the output parameters of the simulation model [3]. All this sometimes leads to the fact that at each subsequent solution of the parameter estimates are scattered so much that lead to uncertainty solutions and in theory, these parameters cannot be calculated. II. Methodology In contrast to the pseudo-random effects using a random process can be theoretically calculated values of the unknown parameters (here can be used by the central limit theorem). In addition, there is no need to correct approach to the selection of averaging intervals as in the study of linear systems and the study of nonlinear systems. In constructing the random number generator (RNG), based on the use of natural sources of stochastic processes, very often there is the problem of choosing relationships between the parameters of the random number sequence and the characteristics of the original random process. The most common block diagram RNG with a uniform distribution is a scheme using a probabilistic binary element (PBE) and the shift register [4, 5]. Binary sequence output PBE generally prepared by polling rate
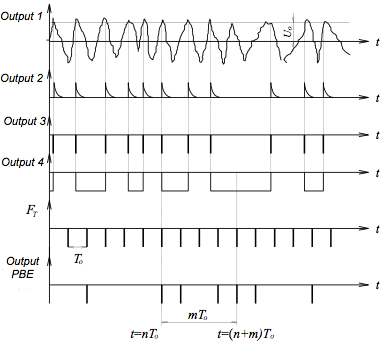
The noise as a narrow-band random process from the noise source 1 receives a threshold device 2 through which the emission of a random process that exceed the set threshold value U0. Emissions that exceed the threshold value offset U0, fed to the amplifier-shaper 3, which are formed on the duration and amplitude. The stream of random pulses from the output of the amplifier-shaper 3 is supplied to the count input of symmetrical trigger 4. If the performance of the amplifier-shaper is sufficient to form each incoming pulse stream of pulses is generated by amplitude and duration to retain the Poisson distribution. The random function
Fig 2. The timing diagram of PBE Realization of these functions are usually called binary sequences. Note that in a case where a sequence of pulses at the input of flip-flop 4 obeys the Poisson distribution, the probability of occurrence of the output PBE units - P and scratch – equal
where
A binary sequence
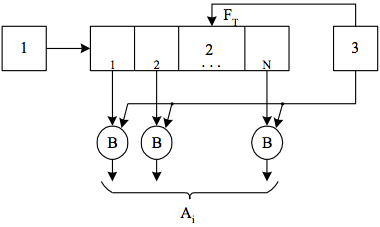
Fig 3. The shift register If we denote
the probability of an N-bit number can be calculated a priori. It will consist of (N-1) and the product multiplied
The minimum probability will have the number A = 101010; or A = 010101, that is:
It is known [1, 2] that the N-bit uniformly distributed binary numbers has an equal probability of 1/2N. Using (2) and (3) one can find the value of the maximum deviation of the distribution law of probabilities N-bit random numbers derived from the binary sequence from uniform. Relative deviation from the uniform can be written as:
Since
The expression on the right side of (4) in a series in the binomial theorem while limiting the first three terms Taking the logarithm of both sides, we finally obtain
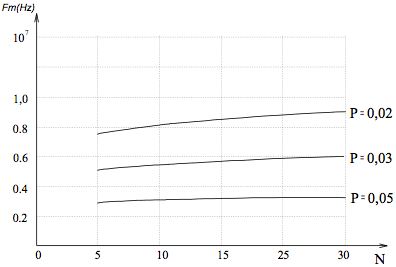
Expression (5) shows what should be the ratio between the average frequency of a Poisson flow and the clock frequency III. Experiments Figure 4 shows a graph of the probability distribution of digital five-digit combination (N = 5) uniformly distributed at random code
Fig 4. Probability distribution of digital five-digit combination Conditions equiprobability appearance PBE digit output can be defined as
If we designate through
where
where k = 1,2,3, ... .. If you are not interested with
Comparing (7) and (6), we have:
How
Expression (8) to evaluate the band amplifier noise, wondering relative deviation of the probability of occurrence of numerical combinations in the PBE output - , the probability of exceeding the threshold U0 in the shaper PBE - P, a clock frequency of random numbers The dependence of the noise bandwidth of the amplifier on the number N of bits of the random number at random
IV. Conclusion The concept of probabilistic binary element provides requirements, which ensure compliance with the criterion of "uniformity" in the implementation of the basic physical generators uniformly distributed random number sequences was proposed. An analytic relation between the parameters of the binary sequence and parameters of a numerical sequence obtained with the shift register output. V. Acknowledgments This work was supported by Russian Ministry of Education and Science in frame of the Federal Program "Research and development on priority directions of scientific-technological complex of Russia Federation in 2014-2020" (contract №14.576.21.0080 (RFMEFI57614X0080)).
|


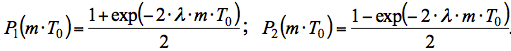
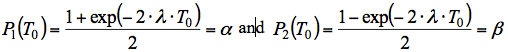 ,
,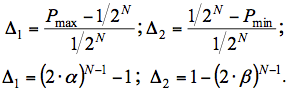
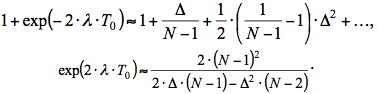
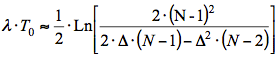 . (5)
. (5)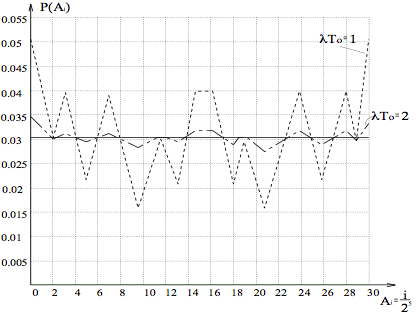
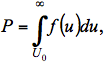
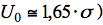 ), we obtain
), we obtain