Улучшенный верифицирующий алгоритм для математической модели взаимных блокировок

Статья опубликована в журнале Международного университета «Дубна» Выпуск 2013 № 3

УДК 004.415.2.052.03, 004.042, 004.046

УЛУЧШЕННЫЙ ВЕРИФИЦИРУЮЩИЙ АЛГОРИТМ ДЛЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ВЗАИМНЫХ БЛОКИРОВОК
Свирин Илья Сергеевич¹, Силин Павел Александрович², Парфилов Иван Васильевич³

¹Кандидат технических наук, генеральный директор;
ООО «Нордавинд-Дубна»;
141980, Московская обл., г. Дубна, ул. Программистов, 4;
e-mail: [email protected].

²Инженер-математик;
«Topcon Positioning Systems»;
115114, г. Москва, Дербеневская наб., 7 (стр. 22);
e-mail: [email protected].

³Инженер-программист;
ФГУП «ЦНИИ ИЭСУ»;
123104, г. Москва, Тверской бул., 7/2;
e-mail: [email protected].

В статье рассматривается алгоритм поиска взаимных блокировок в программном обеспечении на основе его модели. Введено понятие модели взаимных блокировок на основе теории графов, учитывающей понятия субъекта доступа, разделяемого ресурса и средства синхронизации. Приведен верифицирующий алгоритм, заключающийся в сведении систем линейных субъектов к ориентированным графам, вершинами которых являются операторы взаимодействия со средствами синхронизации, а ребра соответствуют соотношениям, возникающим между данными операторами в рамках системы субъектов. Приведено доказательство теорем, подтверждающих работоспособность предложенного алгоритма.

Ключевые слова: многопоточность, взаимные блокировки, верификация программного обеспечения, алгоритм верификации.

IMPROVED VERIFYING ALGORITHM FOR MATHEMATICAL MODEL OF DEADLOCKS
Svirin Ilya¹, Silin Pavel², Parfilov Ivan²

¹Candidate of Science in Engineering, CEO;
Nordavind-Dubna, LLC;
141980, Dubna, Moscow reg., Programmistov str., 4;
e-mail: [email protected].

²Software and Algorithm developer;
«Topcon Positioning Systems»;
115114, Moscow, Derbenevskaya nab., 7 (building 22);
e-mail: [email protected].

³Software developer;
FSUE «CNII EISU»;
123104, Moscow, Tverskoy blvd., 7/2;
e-mail: [email protected].

In article the algorithm of deadlocks searching in software expressed by its model is considered. The concept of deadlocks model based on graph theory considering concepts of the subject (thread), the shared object and the synchronization primitive is introduced. The verifying algorithm conclusing in transformation of linear system of subjects to oriented graphs which nodes are operators of interaction with synchronization primitives is given, and edges correspond to relationships between these operators. The proof of theorems confirming operability of offered algorithm is provided.

Keywords: multi-threading, deadlocks, software verification, algorithm of verification.

Введение

Одной из основных проблем разработки многопоточного программного обеспечения (ПО) является обеспечение доступа различных потоков к разделяемым ресурсам. Для решения данной проблемы современные системы и средства программирования предоставляют средства синхронизации. Однако использование средств синхронизации приводит к проблеме возникновения взаимных блокировок – ситуаций, когда группа потоков не может продолжать выполнение независимо от действий остальных потоков системы. Ошибки, связанные с взаимной блокировкой потоков, чрезвычайно трудно выявить, поскольку их проявление напрямую связано с относительной динамикой выполнения потоков в ПО, зависящей от множества факторов, которые могут проявиться, например, при переходе на новую платформу или добавлении новой подсистемы. Эта особенность делает принципиально невозможным создание алгоритма выявления взаимных блокировок на этапе тестирования ПО.

Существует несколько подходов к решению данной проблемы.
Динамический анализ, который основан на мониторинге выполняющейся программы на предмет обращения к ресурсам и осуществления различных вызовов [2], [8]. Этот подход характеризуется низкими затратами вычислительных ресурсов, однако, обладает большим количеством ложных срабатываний и не гарантирует нахождения всех потенциальных ситуаций блокировки.

Статический анализ использует исходные коды или объектные файлы ПО для построения моделей, которые проверяются на наличие блокировок [1], [3], [4], [5]. Этот подход является достаточно эффективным, хотя порождает большое количество ложных срабатываний и плохо применим к ПО со сложной объектной структурой.

Верификация моделей по методу Model Checking основана на построении формальной модели ПО [10], [11] с последующей верификацией данной модели с помощью специализированных средств [6], [7]. Этот подход принципиально не дает ложных срабатываний и исключает возможность пропуска блокировок, но чрезвычайно требователен к вычислительным ресурсам.

Подход, представленный в данной статье, развивает идеи работы [13] и относится к верификации моделей. Его характерная особенность, являющаяся нетипичной для подходов, связанных с верификацией,  заключается в наглядности представления, достаточной для того, чтобы на основе модели могла быть построена система правил корректного использования средств синхронизации. Применение такой системы правил позволит разработчику ПО избегать появления потенциальных ситуаций взаимной блокировки в процессе проектирования и разработки ПО.

Статья организована таким образом, чтобы дать наиболее полное представление о разработанном авторами подходе. С этой целью приводится краткое описание математической модели взаимных блокировок (раздел 2)  и достаточно полное описание верифицирующего ее алгоритма (раздел 3), которое и является центральной темой статьи.

1. Математическая модель взаимных блокировок

Модель взаимных блокировок в многопоточном ПО включает четыре класса объектов:

1. разделяемый ресурс – информационный или функциональный объект, к которому возможен доступ из разных потоков;
2. субъект доступа – поток, выполняющий доступ к разделяемому ресурсу;
3. средство синхронизации – средство, ограничивающее доступ субъектов к разделяемым ресурсам посредством перевода субъекта в состояние ожидания доступности разделяемого ресурса;
4. взаимная блокировка – ситуация, характеризующаяся тем, что группа субъектов находится в состоянии ожидания и не может быть выведена из него, независимо от действий других субъектов системы.

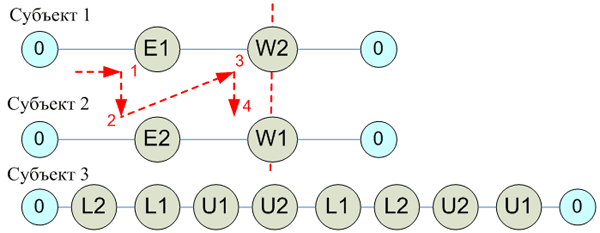
Субъект доступа. Субъект доступа моделируется на основе системы переходов, т.е. субъект отождествляется с совокупностью своих цепочек выполнения. Данная совокупность описывает всевозможные пути выполнения субъекта с точки зрения взаимодействия со средствами синхронизации от «состояния покоя» до «завершающего состояния», отождествляемого с «состоянием покоя».

Отождествление «состояния покоя» и «завершающего состояния» характеризует одно из фундаментальных свойств модели. В ней субъекты доступа «зациклены», т.е. если субъект завершил свое выполнение по некоторому пути выполнения, он не обязательно будет ожидать завершения выполнения остальных субъектов доступа, а может снова начать выполнение по одному из путей.

Для отображения всевозможных путей выполнения, субъект может включать в себя точки ветвления и точки зацикливания (согласно структурной теореме Э. Дейкстры [9]). Отметим, что условие, по которому осуществляется выбор той или иной ветви в точке ветвления, и количество итераций цикла в точке зацикливания не являются существенными с точки зрения модели.

Средства синхронизации. Каждый акт взаимодействия субъекта доступа со средством синхронизации моделируется как выполнение субъектом некоторого оператора, относящегося к средству синхронизации. Средства синхронизации моделируются как совокупность таких операторов. В общем случае в данной модели выделяются четыре примитива синхронизации: нерекурсивный (обычный) исключающий семафор, рекурсивный исключающий семафор (может быть смоделирован на основе нерекурсивного исключающего семафора, поэтому далее не рассматривается), сигнальная переменная с памятью и сигнальная переменная без памяти.

Исключающий семафор – это средство синхронизации, которое в конкретный момент времени может быть захвачено только одним субъектом. Если исключающий семафор захвачен каким-то субъектом, то другой субъект, обращающийся к семафору, переводится в состояние ожидания. Как только семафор освобождается, субъект продолжает свое выполнение. Нерекурсивный (обычный) исключающий семафор описывается двумя операторами взаимодействия – оператором захвата (L_i) и освобождения (U_i), где индекс обозначает номер нерекурсивного семафора.

Сигнальная переменная без памяти – это средство синхронизации, при взаимодействии с которым субъект попадает в состояние ожидания до тех пор, пока другим субъектом не будет отправлен сигнал об освобождении. Сигнал может быть широковещательным, в таком случае он освобождает все ожидающие субъекты, в противном случае – лишь один. Сигнальная переменная без памяти описывается тремя операторами взаимодействия – оператором ожидания (W_i), отправки (E_i) и широковещания (B_i).  

Сигнальная переменная с памятью – это средство синхронизации, обладающее целым неотрицательным счетчиком. Взаимодействие субъекта с сигнальной переменной с памятью приводит к уменьшению счетчика, если счетчик в момент взаимодействия уже равен нулю, то субъект переходит в состояние ожидание до тех пор, пока счетчик не будет увеличен другим субъектом. Сигнальная переменная с памятью описывается двумя операторами взаимодействия – оператором ожидания (A_i) и установки (P_i).

Время выполнения субъектом оператора взаимодействия полагается равным нулю, поскольку не является существенным параметром с точки зрения модели.

На рисунке 1 приводится пример графического изображения системы субъектов.

Взаимные блокировки. Взаимные блокировки моделируются как состояния системы субъектов, в которых возникают ситуации, когда группа субъектов не может продолжать выполнение независимо от действий остальных субъектов системы. На рисунке 1 стрелками показана относительная динамика выполнения субъектов 1 и 2, которая приводит их в состояние взаимной блокировки.

Разделяемые ресурсы. Разделяемые ресурсы присутствуют в данной модели неявно. Они определяются совокупностью средств синхронизации, обеспечивающих синхронный доступ субъектов к разделяемым ресурсам.

Рис. 1. Графическое изображение системы субъектов

Теперь перейдем непосредственно к модели. Формализуем естественное отношение порядка («до» – «после»), возникающее между двумя операторами в рамках одного пути выполнения субъекта. Будем говорить, что i-ый и j-ый исключающие семафоры сравнимы по k-му субъекту, причем i-ый исключающий семафор локально меньше j-го и писать: τ(S_k, L_i) ◄L τ(S_k, L_j), если на пути выполнения k-го субъекту j-ый семафор захватывается до того, как i-ый семафор отпущен после захвата.

Расширим введенную операцию. Будем сравнивать исключающие семафоры, принадлежащие различным субъектам. Будем говорить, что i-ый исключающий семафор k-го субъекта локально меньше j-го семафора m-го субъекта и писать τ(S_k, L_i) ◄L τ(S_m, L_j), если существует такое натуральное    n ≥ 1 и такие субъекты S_x(1),..., S_x(n−1) и исключающие семафоры y(1),..., y(n−1) такие, что:

τ(S_k, L_i) ◄L τ(S_k, L_y(1)),
τ(S_x(1), L_y(1)) ◄L τ(S_x(1), L_y(2)),
...
τ(S_x(n−1), L_y(n−1)) ◄L τ(S_x(n−1), L_y(n)),
τ(S_m, L_y(n)) ◄L τ(S_m, L_j),

где для каждого из субъектов операция ◄L была введена ранее.

Будем говорить, что r-ый исключающий семафор m-го субъекта локально меньше j-ой сигнальной переменной с памятью (без памяти) m-го субъекта и писать τ(S_m, L_r) ◄L τ(S_m, A_j  (W_j)), если взаимодействие с оператором ожидания j-ой сигнальной переменной происходит после захвата r-го исключающего семафора и до его отпускания. В дальнейшем, отсутствие уточнения по поводу принадлежности некоторой сигнальной переменной к переменным без памяти или с памятью означает, что данная переменная может быть произвольного типа.

Будем говорить, что в системе субъектов S = {S₁,..., S_n} i-ая сигнальная переменная находится под локальным влиянием j-ой переменной, если существует субъект S_k из S, путь выполнения которого содержит оператор установки i-ой сигнальной переменной с памятью (оператор отправки или широковещания для переменной без памяти) и оператор ожидания j-ой переменной, либо существует субъект S_k из S, путь выполнения которого содержит оператор установки i-ой сигнальной переменной с памятью (оператор отправки или широковещания для переменной без памяти) и оператор захвата p-го исключающего семафора, причем выполнены следующие условия:

τ(S_k, L_p) ◄L τ(S_m, L_r) и τ(S_m, L_r) ◄L τ(S_m, A_j  (W_j)).

В этом случае будем писать τ(S_k, P_i  (E_i, B_i )) ▼L τ(S_m, A_j  (W_j)), где возможно m = k.

Предположим, что есть система субъектов S = {S₁,..., S_n}, взаимодействующих с сигнальными переменными {1,..., k}. Система субъектов S называется локально слабо упорядоченной по сигнальным переменным, если для любого подмножества {i₁,..., i_j} из {1,..., k} сигнальных переменных не существует такого состояния системы, при которой каждый оператор отправки, широковещания и установки E_u (B_u, P_u), где u из {i₁,..., i_j}, находился бы под локальным влиянием: τ(S_p, E_u (B_u)) ▼L τ(S_q, W_v (A_v)), где v из {i₁,..., i_j}, т.е. все операторы широковещания, отправки и установки из данного множества одновременно находятся под локальным влиянием операторов ожидания из данного множества. Кроме того, в системе не существует сигнальных переменных, для которых присутствуют только операторы ожидания, но нет операторов отправки, широковещания или установки.

Под линеаризацией будем понимать замену цикла точкой ветвления, где одна ветвь содержит цикл точки ветвления, а другая не содержит операторов взаимодействия.

Сформулируем основной результат математической модели взаимных блокировок, который является логическим основанием всех правил корректного использования средств синхронизации на основе данной модели.

Теорема. Пусть имеется система субъектов S = {S₁,..., S_n} с точками ветвления и точками зацикливания. Проделаем для субъектов данной системы линеаризацию по точкам зацикливания. Предположим, что для каждой системы S0 из этого множества выполнены два условия:
1. для любого исключающего семафора (например, j-го) не выполняются соотношения вида τ(Sk0, Lj) ◄L τ(Sm0, Lj)),
2. система S00 слабо локально упорядочена относительно сигнальных переменных.
Тогда в основной системе S нет потенциальных ситуаций взаимной блокировки.

Верифицирующий алгоритм

Теорема о достаточном условии отсутствия потенциальных ситуаций взаимной блокировки в общем случае сводит анализ системы субъектов к анализу системы субъектов, полученных в результате линеаризации из субъектов исходной системы. Следовательно, алгоритм поиска должен быть направлен на анализ систем простых субъектов или субъектов, содержащих только точки ветвления.

Идея, лежащая в основе алгоритма поиска, заключается в сведении системы субъектов к ориентированным графам. Вершинами этих графов будут являться операторы взаимодействия со средствами синхронизации, принадлежащие субъектам данной системы, ребра будут соответствовать соотношениям, возникающим между данными операторами в рамках системы субъектов. Рассмотрим правила, по которым будет строиться это соответствие:

— если два оператора захвата исключающего семафора L_i и L_j принадлежат одному субъекту системы Sk, причем выполнено соотношение τ(S_k, L_i) ◄L τ(S_k, L_j) (т.е. i-ый исключающий семафор локально меньше j-го), то между вершинами, соответствующими операторам L_i и L_j, существует ребро, причем направлено оно от вершины, соответствующей оператору L_i, к вершине, соответствующей оператору L_j;
— если два оператора захвата исключающего семафора L_i и L_i принадлежат субъектам системы S_k и S_m, то между вершинами, соответствующими этим операторам, существует как ребро направленное от одной вершины к другой, так и ребро направленное в обратном направлении, возможно, k = m;
— если оператор захвата исключающего семафора Li и оператор ожидания сигнальной переменной W_j (A_j) принадлежат одному субъекту системы S_k, причем выполнено соотношение τ(S_k, L_i) ◄L τ(S_k, W_j  (A_j)) (т.е. i-ый исключающий семафор локально меньше j-ой сигнальной переменной), то между вершинами, соответствующими операторам L_i и W_j(A_j), существует ребро, причем направлено оно от вершины, соответствующей оператору L_i, к вершине, соответствующей оператору W_j (A_j);
— если субъект системы S_k содержит оператор отправки, широковещания или установки E_i (B_i, P_i), то для каждого оператора захвата исключающего семафора L_j или оператора ожидания сигнальной переменной без памяти (с памятью) W_m (A_m), который так же содержит субъект системы S_k, существует ребро, направленное от вершины, соответствующей оператору E_i (B_i, P_i), к вершине, соответствующей данному оператору (в общем случае возможно i = m);
— если один из субъектов системы S_k содержит оператор ожидания сигнальной переменной без памяти W_i, то для любого оператора E_i (B_i), содержащегося в одном из субъектов системы, существует ребро, направленное от вершины, соответствующей оператору W_i, к вершине соответствующей оператору E_i (B_i) (то же верно для сигнальных переменных с памятью с точностью до замены оператора W_i на A_i и оператора E_i (B_i) на P_i).

Естественность такого соответствия основана на том, что на неформальном уровне направленное от первой вершины ко второй ребро олицетворяет собой зависимость успешного выполнения оператора, соответствующего первой вершине, от успешного выполнения оператора, соответствующего второй. Отсюда следует естественность определения состояния, при попадании в которое гарантированно возникает взаимная блокировка, как замкнутой цепочки зависимостей (т.е. сильно связной компоненты). Введем понятие подозрительных сильно связных компонент, которые будут являться аналогами состояний, при попадании в которые гарантированно возникает взаимная блокировка.

Рис. 2.

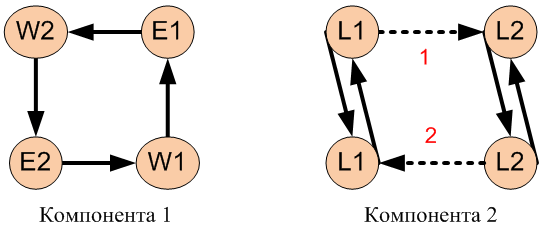
Определение. Ориентированный граф, построенный по системе субъектов S (без точек зацикливания) с использованием только первых двух правил построения ребер, будем называть частным ориентированным графом системы линейных субъектов S. Ориентированный граф, построенный по системе линейных субъектов S с использованием всех пяти правил построения ребер, будем называть общим ориентированным графом системы линейных субъектов S.

Граф, изображенный на рисунке 2, построен по системе субъектов S, представленной на рисунке 1. Отдельно взятая компонента 1 является частным графом системы субъектов S, совокупность компонент 1 и 2 – общим графом системы.

Определение. Будем называть сильно связную компоненту графа, построенного по системе субъектов S (без точек зацикливания), подозрительной сильно связной компонентой 1-го рода, если она содержит операторы захвата хотя бы двух различных исключающих семафоров (например, L_i и L_j).

Определение. Будем называть сильно связную компоненту графа, построенного по системе субъектов S (без точек зацикливания), подозрительной сильно связной компонентой 2-го рода, если она содержит более одной вершины и для некоторого не пустого множества сигнальных переменных {i₁,..., i_n} в нее входят все их операторы отправки, широковещания и установки. Множество {i₁,..., i_n} будем называть множеством сигнальных переменных подозрительной сильно связной компоненты 2-го рода. Будем называть связную компоненту графа, построенного по системе линейных субъектов S, подозрительной связной компонентой 2-го рода, если она содержит более одной вершины и хотя бы один оператор отправки (широковещания или установки).

Отметим, что моделирование на основе графов не учитывает существования соотношений, которые могут не реализовываться в общем состоянии, так как все ребра графа существуют одновременно. В этом отношении предложенный подход теряет свою естественность, поскольку наличие подозрительной сильно связной компоненты может не влечь наличие замкнутой цепочки зависимостей в том случае, если не все ребра этой компоненты (и, как следствие, не все зависимости в замкнутой цепочке) могут реализовываться в некотором общем состоянии. Данное рассуждение приводит к понятию целостности компоненты.

Определение. Сильно связная компонента графа, построенного по системе субъектов S (без точек зацикливания), называется целостной, если существует такое состояние исходной системы S, в котором одновременно реализуются все соотношения, соответствующие ребрам этой компоненты.

Рассмотрим систему субъектов S, изображенную на рисунке 1, и ее общий ориентированный граф, изображенный на рисунке 2. Компонента 1 является целостной, а компонента 2 не обладает этим свойством, поскольку ребра 1 и 2 соответствуют соотношениям, которые не могут быть реализованы в общем состоянии.

Отсюда получается, что если подозрительная компонента является целостной, то замкнутая цепочка зависимостей существует, т.е. обнаружение данной компоненты не будет ложным срабатыванием алгоритма поиска.

Вышеописанные рассуждения приводят к следующей теореме, на которой основан алгоритм.

Теорема. Пусть имеется система субъектов S={S₁,..., S_n} (без точек зацикливания). Пусть в данной системе не выполняются соотношения вида τ(S_k, L_i) ◄L τ(S_k, L_i) и нет сигнальных переменных, обладающих только операторами ожидания и без операторов ожидания. Тогда поиск в системе соотношений вида τ(S_k, L_i) ◄L τ(S_m, L_i) может быть сведен к поиску в частном ориентированном графе системы подозрительных сильно связных компонент 1-го рода. Поиск нарушений слабой локальной упорядоченности системы относительно сигнальных переменных может быть сведен к поиску в общем ориентированном графе системы подозрительных сильно связных компонент 2-го рода. Более того, в обоих случаях поиск не будет иметь ложных срабатываний, если все подозрительные сильно связные компоненты будут целостными.

Доказательство теоремы вытекает из вышеописанных соображений.

Далее приводится описание алгоритма поиска в виде последовательности шагов.

1. Система субъектов S0 подвергается линеаризации по точкам зацикливания. Затем для полученной системы субъектов S применяются остальные шаги алгоритма.
2. По системе субъектов S строится ее частный ориентированный граф. В процессе построения графа выявляется, есть ли в системе отношения вида τ(S_k, L_i) ◄L τ(S_k, L_i) и сигнальных переменных без операторов ожидания или только с операторами ожидания. Наличие соотношений вида τ(S_k, L_i) ◄L τ(S_k, L_i) проверяется при проходе графа путем анализа концов каждого из построенных ребер внутри одного субъекта. Наличие сигнальных переменных проверяется с помощью хранения в памяти переменных, которым недостает соответствующих операторов, и удаления из памяти, когда при проходе графа встречаются соответствующие операторы.
3. С помощью алгоритма Тарьяна [12] граф разбивается на множество сильно связных компонент. Каждая сильно связная компонента анализируется на предмет того, является ли она подозрительной сильно связной компонентой 1-го рода.
4. Все подозрительные компоненты проверяются на предмет ложных срабатываний (проверка целостности). Проверка осуществляется с помощью алгоритма избавления от ложных срабатываний, описанного далее.
5. По системе субъектов S строится ее общий ориентированный граф.
6. С помощью алгоритма Тарьяна ориентированный граф разбивается на связные компоненты. Каждая сильно связная компонента анализируется на предмет того, содержит ли она более одной вершины и хотя бы один оператор отправки (широковещания или установки).
7. С помощью алгоритма Тарьяна каждая подозрительная связная компонента K разбивается на сильно связные компоненты. Каждая сильно связная компонента K⁰ подвергается дальнейшему анализу. Отбираются компоненты, которые содержат операторы отправки (широковещания или установки) сигнальных переменных и состоят более чем из одной вершины.
8. Каждая такая сильно связная компонента K⁰ связной компоненты K подвергается анализу. Если все операторы отправки (широковещания и установки) сигнальных переменных, которые присутствуют в K⁰, лежат в K⁰ (в общем случае они могут лежать в K), то процесс завершается. В противном случае компонента K¹ получается из K⁰ отбрасыванием из нее всех операторов относящихся к переменным, операторы отправки (широковещания или установки) которых лежат в K, но не в K⁰. Далее к компоненте K¹ алгоритм применяется рекурсивно, начиная с шага 6. Процесс завершится, когда будут исключены все сигнальные переменные, либо когда останется сильно связная компонента, которая содержит все операторы отправки (широковещания и установки) сигнальных переменных, которые в ней присутствуют. Такие компоненты назовем подозрительными.
9. Подозрительные сильно связные компоненты 2-го рода проверяются на предмет ложных срабатываний (проверка целостности). Проверка осуществляется с помощью алгоритма избавления от ложных срабатываний, описанного далее.

Теперь опишем процесс избавления от ложных срабатываний. Алгоритм избавления от ложных срабатываний направлен на анализ подозрительных сильно связных компонент 1-го и 2-го родов, которые не обладают свойством целостности. Идея алгоритма заключается в отбрасывании из исходной компоненты ребер до тех пор, пока оставшаяся компонента не станет целостной. Опишем алгоритм в виде последовательности шагов.

1. Из подозрительной сильно связной компоненты K⁰ удаляются все ребра, относящиеся к субъекту S₁. В случае, когда некоторое ребро принадлежит другим субъектам, помимо субъекта, ребра которого удаляются, удаление не производится. Затем из множества ребер, относящихся к субъекту S₁, выделяются всевозможные максимальные подмножества ребер, которые соответствуют реализующимся в общем состоянии соотношениям. Под максимальностью понимается то, что к каждому из этих подмножеств уже нельзя добавить еще одно ребро, чтобы соответствующие им соотношения сохраняли свойства реализуемости в общем состоянии. Затем для каждого такого подмножества его ребра добавляются в граф вместо отброшенных ребер субъекта S₁ (то есть все множество ребер заменили в каждом случае на максимальное подмножество, реализующееся в общем состоянии). Каждая из полученных на этом шаге компонент {K₁¹,..., K_n¹} (а они могут перестать быть даже связными) анализируется на наличие подозрительных сильно связных компонент. Анализ производится методами основного алгоритма, где в роли исходного графа выступает полученные компоненты K_i¹.
2. Анализируются все компоненты K_i¹, полученные на шаге 1, которые содержат подозрительные сильно связные компоненты. На шаге 2 для каждой такой компоненты K_i¹ действия производятся над компонентами субъекта S₂.

Таким образом, в основе алгоритма лежит дерево решений, ветвления которого происходят при переходе к новому субъекту. Ветвь решений заканчивается, когда на некотором шаге полученная компонента K_i^j больше не имеет подозрительных сильно связных компонент. Те ветви, которые содержат подозрительные сильно связные компоненты после последнего N-го шага (в системе субъектов {S₁,..., S_N}), соответствуют действительным срабатываниям.
Непосредственной проверкой можно показать, что сложность алгоритма без проверки на ложность срабатываний есть O(n5), где n – число операторов взаимодействия со средствами синхронизации субъектов исходной системы. При добавлении проверки на ложные срабатывания сложность алгоритма возрастает до O(n^||S||+7), где ||S|| – число субъектов в исходной системе.

Заключение

В данной статье описана математическая модель взаимных блокировок и алгоритм проверки ее корректности (отсутствия в ней взаимных блокировок).

Представленный алгоритм поиска подозрительных сильно связных компонент не является алгоритмом поиска потенциальных ситуаций взаимной блокировки субъектов исходной системы субъектов S. Поскольку, согласно модели взаимных блокировок, отсутствие срабатываний алгоритма гарантирует выполнение условий, необходимых для отсутствия потенциальных ситуаций блокировки в исходной системе субъектов S. Следовательно, представленный алгоритм является алгоритмом проверки выполнения достаточных условий отсутствия потенциальных ситуаций блокировки в системе субъектов S.

Представленный алгоритм является усовершенствованием алгоритма, описанного в работе [13]. Идея, лежащая в основе усовершенствования, заключается в переходе от анализа множества систем, полученных в результате декомпозиции линеаризованной системы по точкам ветвления, к анализу системы, полученной из исходной в результате линеаризации (такие субъекты потенциально могут содержать точки ветвления). Такой подход гарантирует полиномиальную сложность (относительно числа операторов взаимодействия со средствами синхронизации) анализа исходной системы S, поскольку устраняет шаг декомпозиции исходной системы по точкам ветвления, который потенциально может приводить к необходимости анализа экспоненциального числа систем линейных субъектов и, как следствие, экспоненциальной сложности всего алгоритма анализа. Недостаток такого усовершенствования заключается в увеличении числа ложных срабатываний, следовательно, одним из важных направлений усовершенствования всего алгоритма является усовершенствование его части, связанной с отбраковкой ложных срабатываний.

Так же исправлена ошибка, допущенная в работе [13], связанная с неправильным отбрасыванием ребер в части алгоритма, связанной с отбраковкой ложных срабатываний.

Список литературы

1. Artho C., Biere A. Applying Static Analysis to Large-Scale, Multi-threaded Java Programs // 13th Australien Software Engineering Conference, August 2001. – IEEE Computer Society. – 2011. – Pp. 68-75.
2. Bensalem S., Havelund K. Dynamic Deadlock Analysis of Multi-threaded Programs // Haifa Verification Conference, Springer, 2005. – Vol. 3875. – Pp. – 208-223.
3. Detlefs D. L., Rustan K., Leino M., Nelson G., Saxe J. B. Extended Static Checking // Technical Report 159, Compaq Systems Research Center, Palo Alto, California, USA, 1998.
4. Engler D., Ashcraft K. RacerX: Effective, Static Detection of Race Conditions and Deadlocks // Proceedings of the 19th ACM Symposium on Operating Systems Principles, October 2003. – Pp. 237-252.
5. Havelund K., Pressburger T. Model Checking Java Programs using JavaPathFinder // International Journal on Software Tools for Technology Transfer, 2(4):366–381, April 2000. Special issue of STTT containing selected submissions to the 4th SPIN workshop. – Paris, France, 1998.
6. Holzmann G. Design and Validation of Computer Protocols. – Prentice Hall, 1991.
7. Lamport L. Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers. – Addison-Wesley, 2002.
8. Savage S., Burrows M., Nelson G., Sobalvarro P., Anderson T. Eraser: A Dynamic Data Race Detector for Multi-threaded Programs // Proceedings of the 16th ACM Symposium on Operating Systems Principles, October 1997. – Pp. 27-37.
9. Дал У., Дейкстра Э., Хоор К. Структурное программирование = Structured Programming. 1-е изд. – М.: Мир, 1975.
10. Кларк Э., Грамберг О., Пелед Д. Верификация моделей программ: Model Checking. – М.: МНЦМО, 2002.
11. Карпов Ю. Model Checking верификация параллельных и распределенных программных систем. – СПб.: БХВ-Петербург, 2010.
12. Седжвик Р. Фундаментальные алгоритмы на С++. Алгоритмы на графах: Пер. с англ. – СПб: ООО «ДиаСофтЮП», 2002.
13. Парфилов И. В., Свирин И. С., Силин П. А., Шумилов Ю. Ю. Верифицирующий алгоритм для математической модели взаимных блокировок. Спецтехника и связь, ISSN 2075-7298, выпуск 6,  с. 28-33, ноябрь-декабрь 2011.