- Главная
- О Группе компаний
- Продукты
- Безопасность
- Комплексная автоматизированная информационная система «Безопасный город»
- ПО потокового вещания видео и ведения архива «Медиасервер»
- ПО для создания распределенных систем IP-видеонаблюдения «SmartStation»
- Программно-аппаратный комплекс для создания систем видеонаблюдения «ТелеВизард-HD»
- ПО для создания систем видеонаблюдения «Компас»
- Здоровье
- Блокчейн
- Безопасность
- Наука
- Отзывы
- Контакты


Сверточная нейронная сеть для распознавания символов номерного знака автомобиляСтатья опубликована в журнале Международного университета «Дубна» Выпуск 2013 № 3 УДК 002:004.9 СВЕРТОЧНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ РАСПОЗНАВАНИЯ СИМВОЛОВ НОМЕРНОГО ЗНАКА АВТОМОБИЛЯ 1Аспирант, разработчик; В работе рассматривается подход к распознаванию изображений символов автомобильного номера на основе сверточных нейронных сетей (СНН, convolutionalneuralnetwork). Использование сверточных нейронных сетей для распознавания изображений обусловлено двумя основными факторами: 1) снижение сложности нейронной сети и сложности ее обучения, в сравнении с классическим многослойным персептроном, что актуально в области обработки и анализа изображений; 2) повышение устойчивости распознавания к различным к искажениям символов в сравнении с классическими нейронными сетями и другими методами классификации изображений. В работе описывается процесс разработки сверточной нейронной сети для распознавания изображений символов автомобильного номера. В завершении проводится сравнения качества разработанного метода и метода на основе сопоставления шаблонов (templatematching). Ключевые слова: свертка, нейронные сети, нейрон, алгоритм обратного распространения ошибки, выборка, классификатор. CONVOLUTIONAL NEURAL NETWORK FOR RECOGNITON OF LICENCE PLATE SYMBOLS 1Aspirant, developer; This paper discusses an approach to the license plate character recognition based on convolutional neural networks (CNN, convolutional neural network). Using a convolutional neural network for image recognition is caused by two main reasons: 1) reduction of the complexity of the neural network training and output calculation in comparison with a classical multilayer perceptron, which is important in the field of image processing and analysis, and 2) increased robustness of CNN to different distortion applied to symbols recognition in contrast to classical neural networks and other methods of image classification. The paper describes the design process of the convolution neural network for recognition of license plate characters. At the end conducted comparing the quality of the developed CNN recognition method and traditional template matching method. Keywords: neural network, neuron, backpropagation algorithm, sample, classifier. ВведениеЗадача автоматического распознавания автомобильных номеров на цифровых изображениях и видео уже решена многими исследователями, но по-прежнему актуальна из-за отсутствия достаточной для многих прикладных программно-аппаратных систем эффективности решения задачи распознавания. Системы распознавания автомобильных номеров, как правило, используются для контроля въезда/выезда автотранспорта с территории предприятий, парковок, контроля потока автомобильного трафика. Они могут размещаться в службах автоинспекции, на контрольно-пропускных пунктах, пунктах контроля скорости и т.д. Алгоритмы распознавания номерных знаков в таких системах должны быть устойчивыми к искажениям изображений номерных пластин, вызванных: различной скоростью движения транспортных средств, различным расположением камеры относительно номерного знака транспортного средства, дефектами пластины автомобильного номера (загрязнение, деформация), а также изменениями в условиях внешнего освещения. Кроме того, сами номерные знаки отличаются в рамках различных классификаций: номерные знаки государственных служб, такси, номерные знаки иностранных автомобилей, номерные знаки легковых, грузовых и других транспортных средств. Это также необходимо учитывать в построении прикладной системы распознавания номеров. Процесс решения задачи распознавания автомобильного номера может быть разбит на несколько последовательно выполняемых подпроцессов. Общая схема решения задачи приведена на рис.1.
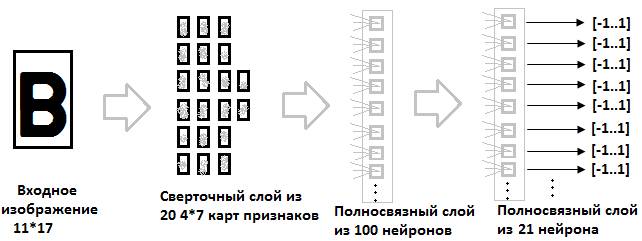
Каждый из этапов, изображенных на рис.1. может быть выполнен различными способами и с разной степенью эффективности. В этой работе мы рассматриваем только этап «Классификация сегментов пластины автомобильного номера» (на рис.1. он выделен в прямоугольник со скругленными углами), связанный с непосредственным распознаванием символов номера. Несмотря на то, что на эффективность алгоритма распознавания символов напрямую оказывают влияние результаты выполнения предыдущих этапов, но в данной статье мы не будем рассматривать эти этапы ввиду их выхода за рамки проблематики, охватываемой в данной работе и ограничения объема статьи. Распознавание символов мы будем осуществлять с помощью сверточной нейронной сети [1]. Рассмотрим структуру и свойства сверточной нейронной сети для распознавания символов номера. 1. Сверточная нейронная сеть для распознавания символов автомобильного номераИспользование классических нейронных сетей для распознавания изображений затруднено, как правило, большой размерностью входной вектора входных значений нейронной сети, большим количеством нейронов в промежуточных слоях и, как следствие, большими затратами вычислительных ресурсов на обучение и вычисление сети. Приведем пример. Пусть имеем входное изображение 25*25 пикселей, т.е. 625 нейронов во входном слое. Количество нейронов скрытых слоев нейронной сети обычно выбирается в 10-20 раз больше количества входных значений нейронной сети. Пусть наша нейронная сеть состоит из двух скрытых слоев. Первый скрытый слой состоит из 6000 нейронов (и 3,75 млн. связей с входным слоем), а второй из 3000 нейронов (и 18 млн. связей с первым скрытым слоем). Полный набор символов номерных знаков состоит из 24 символов, т.е. в выходном слое имеем 24 нейрона и 72000 связей с предыдущим слоем. Каждая связь между нейронами имеет настраиваемый параметр — вес, для которого в процессе обучения нейронной сети вычисляется градиент ошибки. Из приведенного примера видно, что задача вычисления и обучения нейронной сети для распознавания изображений исключительно сложная. Кроме того, в распознавании визуальных образов часто требуется классификация изображений, превышающих размер 25*25 пикселей из приведенного примера. Еще одним минусом классических нейронных сетей является отсутствие возможности учитывать топологию входного изображения, т.е. информацию о взаимном расположении пикселей изображения. Сверточным нейронным сетям в меньшей степени присущи описанные выше недостатки. Ключевым моментом в понимании сверточных нейронных сетей является понятие так называемых «разделяемых» весов, т.е. часть нейронов некоторого рассматриваемого слоя нейронной сети может использовать одни и те же весовые коэффициенты. Нейроны, использующие одни и те же веса, объединяются в карты признаков (feature maps), а каждый нейрон карты признаков связан с частью нейронов предыдущего слоя. При вычислении сети получается, что каждый нейрон выполняет свертку (операцию конволюции) некоторой области предыдущего слоя (определяемой множеством нейронов, связанных с данным нейроном). Слои нейронной сети, построенные описанным образом, называются сверточными слоями. Помимо, сверточных слоев в сверточной нейронной сети могут быть слои субдискретизации (выполняющие функции уменьшения размерности пространства карт признаков) и полносвязные слои (выходной слой, как правило, всегда полносвязный). Все три вида слоев могут чередоваться в произвольном порядке, что позволяет составлять карты признаков из карт признаков, а это на практике означает способность распознавания сложных иерархий признаков [1-3]. В данной работе мы рассматриваем сверточную нейронную сеть для изображений символов автомобильного номера размерностью 10*16 пикселей (16 строк и 10 столбцов). В соответствии с [4] перед подачей изображения на вход нейронной сети необходимо увеличить размерность изображения (добавлением «пустых» пикселей) так, чтобы количества строк и столбцов были нечетными. Таким образом, входной слой нейронной сети содержит 11*17 = 187 нейронов. Общая структура сети изображена на рис.2.
Структура нейронной сети (рис. 2) была подобрана экспериментально. Расширенное на одну строку и один столбец входное изображение, содержащееся в первом слоев, подается на вход сверточному слою, состоящему из 20 карт признаков размером 4*7 каждая. Таким образом, сверточный слой содержит 4*7*20 = 560 нейронов. Каждый нейрон выполняет операцию свертки части входного изображения с ядром 5*5. Таким образом, каждой карте признаков соответствует 5*5 = 25 весов и 1 смещение. Итого, (5*5 + 1)*20 = 520 весов и (5*5 + 1)*560 = 14560 связей в сверточном слое. Так как каждый нейрон из некоторой произвольно выбранной карты признаков выполняет свертку с ядром 5*5 части изображения размером 5*5 пикселей, то все изображение разбивается на перекрывающиеся области 5*5 пикселей. Перекрытие составляет 3 пикселя, отсюда по вертикали имеем 7 областей 5*5 пикселей, по горизонтали 4 области 5*5 пикселей, отсюда, размерность карты признаков — 4*7 нейронов. Выходные значения нейронов сверточного слоя подаются на вход полносвязному слою, состоящему из 100 нейронов, 100*(560 + 1) весов и такого же количества связей (в полносвязном слое каждой связи между нейронами соответствует уникальный весовой коэффициент). Выходной слой также является полносвязным и состоит из 21 нейронов (101*21 = 2121 связей и весов), соответствующих используемому набору символов. Из полного набора (24 символа) мы исключили символы 'D' и 'Z', т.к. они не используются в российских номерах, а также символ 'O' из-за того, что после сегментации номерной пластины символы '0' и 'O' практически неотличимы (разграничение классов символов '0' и 'O' можно осуществлять семантически уже на этапе синтаксико-семантического анализа). Полный набор символов выглядит так: Выходной вектор нейронной сети состоит из 21 вещественного значения из отрезка [-1,1]. В идеальном случае, все выходные значения должны быть равны -1, кроме значения, соответствующего классу входного изображения — оно должно быть равно +1. Обучение нейронной сети требует качественной и большой выборки. В следующем разделе мы рассматриваем процесс подготовки тренировочной и тестовой выборок символов автомобильного номера. 2. Подготовка тренировочной и тестовой выборокПодготовка тестовой выборки Символы автомобильного номера для тестовой выборки были извлечены с помощью вывода промежуточных результатов работы программной системы «ТелеВизард-Авто», разрабатываемой компанией ООО «Нордавинд». «ТелеВизард-Авто» — программный продукт, предназначенный для распознавания автомобильных номеров на контрольно-пропускных пунктах. Схема работы алгоритма системы соответствует схеме, приведенной на рис.1. С помощью видеокамеры система осуществляет захват изображений, содержащих автомобиль. Далее производится предварительная обработка изображения и выделение номерной пластины, результаты этих этапов передаются на вход алгоритму сегментации номерной пластины. После этапа «Сегментация пластины автомобильного номера» мы имеем набор изображений символов, которые затем передаются на вход алгоритму распознавания символов. Именно эти изображения мы используем в качестве тестовой выборки. Примеры изображений символов автомобильного номера, извлеченных с помощью «ТелеВизард-Авто» приведены на рис.3.
Из рис.3. видно, что изображения символов сильно зашумлены, даже для человека не всегда легко определить однозначно, какой символ изображен. После извлечения символов, каждому изображению выборки была поставлена в соответствие метка класса символа — целое число от 0 до 20 (класс 0 соответствует символу '0', класс 1 соответствует символу '1' и т.д.). Если не удалось определить, что за символ включает изображение, это изображению выставлялся в соответствие произвольный класс. В итоге, мы подготовили 6378 пары изображение/метка класса. Описанный выше процесс присвоения изображения меток классов длителен и трудоемок, а размер тренировочной выборки должен быть гораздо больше, чем размер тестовой выборки. Поэтому было принято решение выполнить генерацию различных изображений с помощью возмущений и шумов, искусственно вносимых в некоторые эталонные изображения символов автомобильных номеров. В качестве эталонных изображений символов мы использовали растровые изображения символов шрифта, используемого при производстве автомобильных номеров (согласно ГОСТ Р 50577-93). Рассмотрим подробно процесс генерации тренировочной выборки. Подготовка тренировочной выборки Генерация тренировочной выборки осуществлялась путем применения искажающих преобразований к изображениям оригинальных символов шрифта, используемого в автомобильных номерах. Изображения символов шрифта предварительно приводились к размеру 10*16 пикселей. Изображения символов шрифта, используемого в автомобильных номерах с размером 10*16 пикселей, показаны на рис.4.
К изображениям с рис.4 были применены следующие искажающие преобразования:
Таким образом, применяя описанные выше преобразования, мы получили 184233 изображений тренировочной выборки. Примеры этих изображений приведены на рис.5.
Преимущество такого способа подготовки выборки состоит в отсутствии необходимости вручную проставлять метки классов изображений, т.к. всегда известно изображение какого символа мы обрабатываем в данный момент. Для того, чтобы показать эффективность разрабатываемого метода распознавания символов на основе сверточной нейронной сети, рассмотрим более простой способ распознавания символов: метод сопоставления шаблонов. Результаты работы этих методов мы будем сравнивать по качеству распознавания на тестовой выборке. 3. Метод сопоставления шаблонов для распознавания символовМетод распознавания символов с помощью сопоставления шаблонов предполагает наличие шаблонов для всех возможных изображений символов. Принятие решения о принадлежности текущего изображения символа, извлеченного из автомобильного номера на этапе сегментации, к определенному классу символов осуществляются по критерию минимума (максимума) некоторой метрики сходства изображения символа и его шаблона. В этой работе мы использовали шаблоны символов, где каждому пикселю изображения 10*16 ставится в соответствие число от 0 до 5. Пиксели шаблона, соответствующие пикселю символа, помечаются нулевыми значения, а пиксели, не принадлежащие символу (пиксель фона), помечаются значениями 1-5 в зависимости от удаленности пикселя фона от ближайшего пикселя символа, а также субъективной «важности» пикселя с точки зрения дифференциаций различных классов символов. Примеры используемых шаблонов символов приведены в табл.1. Табл.1. Примеры шаблонов символов, используемых при распознавании методом сопоставления шаблонов
Текущее изображения символа номера относится к тому классу символов, значение корреляции с шаблоном которого — максимально. То есть метрикой в данном конкретном случае служит коэффициент корреляции (точнее абсолютное значение коэффициента корреляции). Формула для еговычисления приведена ниже:
где Преимущества этого подхода к распознаванию изображений символов — в высокой скорости алгоритма классификации и его простоте. Недостаток — отсутствие устойчивости к искажениям символов. Этот подход, как уже говорилось выше, приведен для сравнения с подходом на основе нейросетевого классификатора, результаты моделирования работы которого приведены в следующем разделе. 4. Обучение нейронной сети и результаты моделированияОбучение нейронной сети выполнялось на тренировочной выборке, состоящей из 184233 изображений символов. Изображения тестовой выборки символов (6378) не участвовали в обучении. В качестве алгоритма обучения использовался алгоритм обратного распространения ошибки. В соответствии с [3] для ускорения обучения использовался стохастический варианта метода Левенберга-Марквардта. Обучение проводилось в течение 60 эпох. Нейронная сеть достигла способности распознавать все изображения, кроме 515 из 184233 (т.е. ошибка составляет 0,28%). Тестирование нейронной сети проводилось на изображениях тестовой выборки: ошибка распознавания составила 11,8% (751 изображение из 6378). Моделирование работы метода распознавания символов на основе сопоставления шаблонов показало ошибку 23,1% (1475 символов не распознано из 6378 изображений). Таким образом, на тестовой выборке нейронная сеть правильно распознала почти в два раз больше изображений символов автомобильного номера, чем метод на основе сопоставления шаблонов. ЗаключениеВ работе были рассмотрены два метода распознавания символов: метод на основе сопоставления шаблонов и метод на основе сверточной нейронной сети. Описана общая структура сверточной нейронной сети, а также приведена структура частной сверточной нейронной сети, используемой для решения задачи распознавания изображений символов автомобильного номера размерностью 10*16 пикселей. Приведено краткое описание процесса обучения нейронной сети, включая подготовку тестовой выборки и генерацию тренировочной выборки. В завершение, приведены результаты тестирования обоих описанных методов распознавания на одной и той же тестовой выборке. По результатам тестирования, метод на основе сверточной нейронной сети превзошел метод на основе сопоставления шаблонов в 1,96 раз по точности распознавания на тестовой выборке. Необходимо отметить, что при обучении нейронной сети использовалась «искусственно» сгенерированная тренировочная выборка. Использование «естественной» выборки, т.е. выборки, полученной алгоритмами сегментации конкретной программно-аппаратной системы распознавания номеров, позволило бы добиться гораздо лучших результатов распознавания изображений символов, но создание такой выборки потребовало бы гораздо больше времени. Список литературы
|



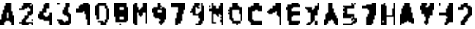
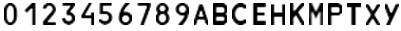
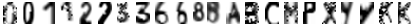
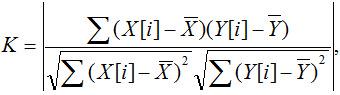 (1)
(1)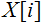 и
и 



